在同等情况下,光伏电站中合理且更高的光伏组件串联数可以节约电缆用量、支架用量及逆变器数量,同时还能够降低线损,提高光伏电站的整体发电效率。目前在光伏电站设计中,光伏组件串联数的计算广泛采用 GB 50797-2012《光伏发电站设计规范》[1] 或 IEC 62548-2016《Photovoltaic (PV) arrays——Design requirements》[2] 中的计算方式,即假定在极端环境低温的情况下对光伏组串的开路电压、最大功率点电压等进行计算,进而确定光伏电站的光伏组件串联数。陈智 [3]、周长友等 [4] 从技术经济性的角度给出了在国内部分城市建设光伏电站时推荐的光伏组件串联数。国内外学者 [5-8] 对于光伏组件的开路电压、最大功率点电压,以及光伏组件串、并联电阻等的计算也都提出了很多方法。另外,邢广成等 [9] 根据太阳电池的工作原理,建立了以太阳电池为基础的等效数学模型,从而能够近似得到光伏阵列在某太阳辐照度和环境温度条件下的输出特性。孟海凤等[10]提出了太阳电池 I-V 特性参数的校准方法,该方法可以分析太阳辐照度、环境温度等因素对太阳电池关键性能的影响。
但随着光伏行业竞争的加剧,对光伏电站度电成本的要求日益严苛,此种形式下,当前国家标准对于光伏电站中光伏组件串联数的计算方式已经偏于保守,且完全从极端环境低温的角度出发来考虑太阳辐照度对环境的温升作用同样偏于保守。在最新版的 IEC 62738-2018《Ground mounted photovoltaic power plants——Design guidelines and recommendations》中提出了改进后的光伏电站光伏组件串联数的计算方式,不再要求采用极端环境低温进行计算,而是允许在数据足够充分的情况下采用限制在日照时间内的年平均最低环境温度进行计算。
除国家标准给出的光伏组件串联数的计算方法之外,业内众多逆变器厂家、光伏组件厂家、设计院等也都采用自身产品建设了实验光伏电站,通过对实验光伏电站进行实际观测得到了环境温升与太阳辐照度的关系,以及光伏组件温升与环境温升及太阳辐照度的关系,并在此基础上假设极端环境低温对应最低太阳辐照度,太阳辐照度与环境温度成正比关系,环境温度升至最高值时对应的太阳辐照度也达到最大值,以此对光伏电站的光伏组件串联数进行了修正计算。虽然这种计算方式能在一定程度上修正光伏组件串联数,但这种修正方式依然存在弊端,即由于各个地区的气候情况不一,完全用线性关系或某个地区的实验数据替代环境温度与太阳辐照度的关系会使计算结果存在较大误差。
基于此,研究环境温度与太阳辐照度的关系,并在此基础上进行光伏电站的光伏组件串联数的计算是有必要的。本文依据近期国际上超大型的光伏发电项目中光伏电站的光伏组件串联数计算的经验,以中东地区某光伏发电项目为例,提出了一种以大量气象数据为基础来预测最低环境温度与太阳辐照度的关系,并在此基础上联合计算光伏组串的开路电压与最大功率点电压,从而确定光伏电站中光伏组件串联数的优化计算方法。
1 研究对象
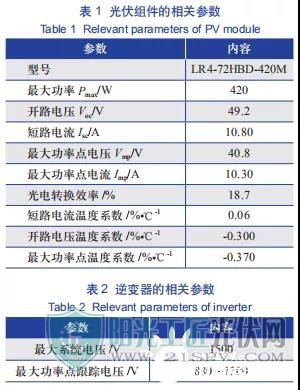
本文以中东地区卡塔尔的某交流侧装机容量为 900 MW 的光伏电站为例进行相关计算。项目所在地的地理坐标为 25.26°N、50.94°E,海拔为 25 m;极端环境低温为 -5 ℃,极端环境高温为 50 ℃。该光伏电站采用双面单晶硅光伏组件( 尺寸为 2131 mm×1052 mm×40 mm),标准测试条件 (STC) 下,光伏组件的相关参数如表 1 所示,逆变器的相关参数如表 2 所示。
2 计算方法
2.1 计算流程
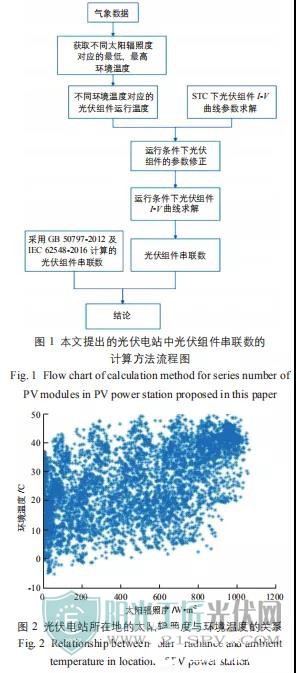
本文提出的光伏电站中光伏组件串联数的计算方法是利用太阳辐照度对应的最低环境温度对光伏组件串联数进行优化设计。具体计算流程如图 1 所示。
2.2 气象数据的选择
本光伏电站光伏组件串联数的计算方法采用的气象数据选择 SolarGIS 辐照气象数据库的逐时数据。该光伏电站所在地的太阳辐照度与环境温度的关系如图 2 所示。
2.3 光伏组件运行温度的计算
计算光伏组件运行温度 Tcell 的公式为:
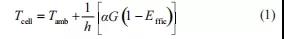
式中,Tamb 为环境温度,K;h 为热交换系数,W/(m2?K);Effic 为光伏组件的光电转换效率;α 为太阳辐照吸收系数,通常取值为 0.9;G 为光伏组件接收的太阳辐照度,W/m2。
2.4 光伏组件工程模型
2.4.1 光伏组件的 I-V 特性曲线根据光伏组件的单二极管等效电路模型 [8,11],STC 下光伏组件的 I-V 曲线关系可表示为:
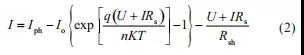
式 中,I 为 光 伏 组 件 的 输 出 电 流,A;I o 为光伏组件反向饱和电流,A;U 为光伏组件的输出电压,V;q 为电荷常数,此处取 1.602×10-19 C;n 为二极管品质因子;K 为Blotzman 常数,此处取 1.381×10-23 J/K;T 为光伏组件绝对工作温度,K;Rs 为光伏组件的串联电阻,Ω;Rsh 为光伏组件的并联电阻,Ω;Iph为光生电流,A。
2.4.2 不同运行条件下的光伏组件的参数
计算光伏电站中光伏组件串联数时涉及的参数主要为 Voc、Isc、I mp、V mp,可分别通过公式 (3)~公式 (6)[7] 计算得出,即:
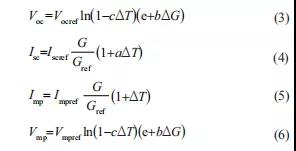
式中,a、b、c 均为拟合系数,通常取值为a=0.0025/℃,b=0.0005 (W/m2)-1,c=0.00288/℃;e为自然常数;ΔG 为实际太阳辐照度与参考太阳辐照度 (1000 W/m2) 之间的差值,W/m2;ΔT 为光伏组件实际工作温度与参考工作温度 (25 ℃)之间的差值,K;Vocref 为 STC 条件下光伏组件的开路电压,V;Iscref 为 STC 条件下光伏组件的短路电流,A;Gref 为 STC 条件下的太阳辐照度,取值为 1000 W/m2;Impref 为 STC 条件下光伏组件的最大功率点电流,A;Vmpref 为 STC 条件下光伏组件的最大功率点电压,V。
3 计算结果及分析
3.1 极端环境温度预测的误差分析
为获取同一太阳辐照度对应的最低环境温度和最高环境温度,采用临近点比较法,以获取某一太阳辐照度区间内的所有环境温度值,并将最小值和最大值进行拟合,从而可得到太阳辐照度分别与最低环境温度和最高环境温度的包络曲线,具体如图 3 所示。
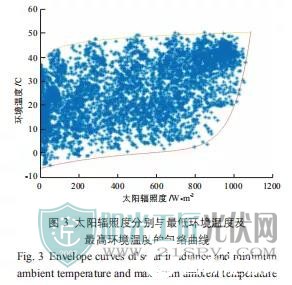
由于环境温度随着太阳辐照度的增加而增加,因此从图 3 中的包络曲线可以看出,在太阳辐照度较高的区域,环境温度也较高。
对相同太阳辐照度对应的最高环境温度和最低环境温度包络曲线与数据进行对比,可得到极端环境温度的最大误差为 1.63 ℃,然后可计算得出此误差对光伏组件开路电压的影响为 0.24 V;按照每个光伏组串串联 40 块光伏组件来计算,累计误差仅为9.6 V,相对误差仅为0.489%。因此,可以认为利用拟合曲线来计算光伏组串开路电压时所得到的计算结果在合理的误差范围 ( 行业内一般设定为 6%) 内。
3.2 光伏组件电压的计算
利用图 3 所示的太阳辐照度与极端环境温度包络曲线,可以计算出不同太阳辐照度下光伏组件的电压。
3.2.1 光伏组件开路电压与太阳辐照度的关系
在实际的最低环境温度情况下,光伏组件开路电压与太阳辐照度的关系如图 4 所示。
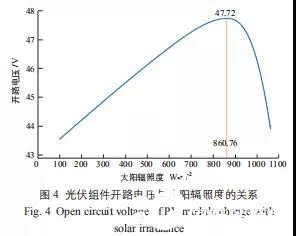
综合图 3 和图 4 可以看出,当太阳辐照度较高时,对应的最低环境温度较高,此时光伏组件的开路电压反而比 STC 下光伏组件的开路电压(49.2 V) 有所降低,而非 GB 50792-2012 与 IEC 62548-2016 所描述的“在最强的太阳辐照度及所在地极端环境低温情况下计算得到的光伏组件开路电压升高”。利用环境温度对本项目所在地的参数条件进行修正后可以看出,光伏组件开路电压最大值出现在太阳辐照度为 860.76 W/m2 时,最大值为 47.72 V。
研究者对不同地区的数据进行分析后发现,不同地区的光伏组件开路电压最大值对应的太阳辐照度值也不同。在高纬度地区,由于平均环境气温较低,因此光伏组件开路电压最大值对应的太阳辐照度可能低于 400 W/m2;在低纬度地区,光伏组件开路电压最大值对应的太阳辐照度可能接近 1000 W/m2。
在本项目所在地的气候条件及所选的设备条件下,光伏组件开路电压的影响因素主要有 2 个方面:一方面是由于环境温度升高,导致光伏组件开路电压降低;另一方面是由于太阳辐照度升高,导致光伏组件开路电压升高。从图 4 可以看出,当太阳辐照度超过 860.76 W/m2 后,其对“由环境温度提升导致的光伏组件开路电压降低”的影响超过了对“由太阳辐照度直接导致的光伏组件开路电压升高”的影响。因此图 4 中的曲线整体呈现光伏组件开路电压随着太阳辐照度的增加呈现先增加而后降低的趋势。
3.2.2 光伏组件工作电压与太阳辐照度的关系
若要通过光伏组件工作电压来确定光伏组件串联数,则需要根据最高环境温度与最低环境温度条件下计算得到的光伏组件工作电压来共同确定,具体方法如下。
1) 按最高环境温度计算的光伏组件工作电压。图 5 为按最高环境温度计算的光伏组件工作电压与太阳辐照度的关系曲线。
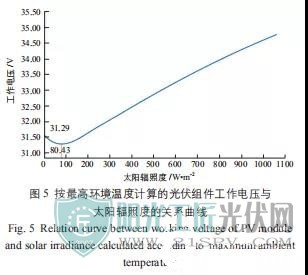
由图 5 可知,按最高环境温度计算光伏组件工作电压时,环境温度与光伏组件工作电压呈现负相关。根据图 3 的结论,随着太阳辐照度增加,环境温度增加,且在太阳辐照度较低的区域最高环境温度增加较快。因此,在太阳辐照度较低的区域,“由于太阳辐照度升高导致光伏组件工作电压提升”造成的影响小于“由于太阳辐照度增加导致环境温度升高,从而导致光伏组件工作电压降低”造成的影响。从图 5 的曲线来看,随着太阳辐照度的增加,光伏组件工作电压呈现先降低后增加的趋势;光伏组件工作电压最小值出现在太阳辐照度为 80.43 W/m2时,最小值为 31.29 V。
2) 按最低环境温度计算的光伏组件工作电压。图 6 为按最低环境温度计算的光伏组件工作电压与太阳辐照度的关系曲线。
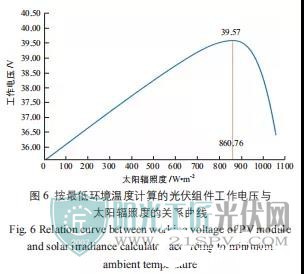
如图 6 所示,按最低环境温度计算光伏组件工作电压时,光伏组件工作电压随着太阳辐照度的增加呈现先增加后降低的趋势。从图 3 的结论可以看出,在太阳辐照度较高的区域,环境温度的曲线上升很快。由于太阳辐照度升高导致光伏组件工作电压升高,环境温度升高导致光伏组件工作电压降低。因此在太阳辐照度较高的区域,“由于太阳辐照度的升高导致环境温度升高,从而导致光伏组件工作电压降低”造成的影响超过了“由于太阳辐照度升高直接导致光伏组件工作电压升高”造成的影响。光伏组件工作电压最大值出现在太阳辐照度为 860.76 W/m2 时,最大值为 39.57 V。
3.3 光伏组件串联数的计算
根据前文的分析,基于最新标准 IEC 62738-2018 中的公式,采用本文的优化方法计算光伏组件串联数 N,可以得到 N 值的 3 个范围,即 N ≤ 1500/47.72=31.4、N ≥ 880/31.29=28.12、 N≤1300/39.57=32.85。对这 3 个结果进行综合考虑后,可得到光伏组件串联数 N 为 29~31 块。
而在同等条件下,若采用 GB 50797-2012 或IEC 62548-2016 要求的极端环境温度情况计算,利用 PVsyst 软件可计算得到光伏组件串联数 N 为 25~27 块。
从以上的结果可以看出,采用优化计算得到的单串光伏组串最大可串联的光伏组件数提高了14.8%,即同样长度的电缆可接入的光伏组件数增加了 14.8%,因此在光伏电站总装机容量不变的情况下,本优化设计可节省大量电缆,度电成本也将随之降低。同时,由于单串光伏组串可串联的光伏组件数增加,即同等电缆用量时可接入的光伏组件数增加,在实际运行情况下,光伏组串内工作电流不变,但是光伏专用电缆内输送的电压更高,则直流线损可减少 12.9%。因此,本优化设计对提高光伏电站的系统效率 PR 有显著作用。
4 结论
本文以中东地区某光伏发电项目为例,在气象数据足够准确的情况下,提出了一种以大量气象数据为基础来预测环境温度与太阳辐照度的关系,并在此基础上联合计算光伏组串的开路电压与最大功率点电压,从而确定光伏电站的光伏组件串联数的方法;然后将该优化计算方法得出的光伏组件串联数结果与采用 GB 50797-2012 或 IEC 62548-2016 中根据太阳辐照度对极端环境温度进行修正计算的方法得到的光伏组件串联数结果进行了对比,得到以下结论:
1) 本优化计算方法可以显著提高光伏组件串联数,在中纬度地区,单串光伏组串的最大光伏组件串联数可提高 2~4 块。
2) 本优化计算方法可以节省电缆,在中纬度地区,单串光伏组串所用电缆用量可节省 14.8%。
3) 本优化计算方法可以降低直流线损,同等电缆用量时可接入的光伏组件数增加,从而光伏组串内电流不变,但是输送容量增加,从而直流线损可减少 12.9%,因此对提高光伏电站的系统效率 PR 有显著作用。在相同装机容量且其他条件不变的情况下,电缆用量降低,光伏电站的度电成本也将随之降低。
原标题:光伏电站中光伏组件串联数的优化设计

 扫描关注微信
扫描关注微信






 宁德时代吴凯...
宁德时代吴凯... 天合光能陈奕...
天合光能陈奕... 刘岩: 追光行...
刘岩: 追光行... 黄震院士:大...
黄震院士:大...